simulated-annealing
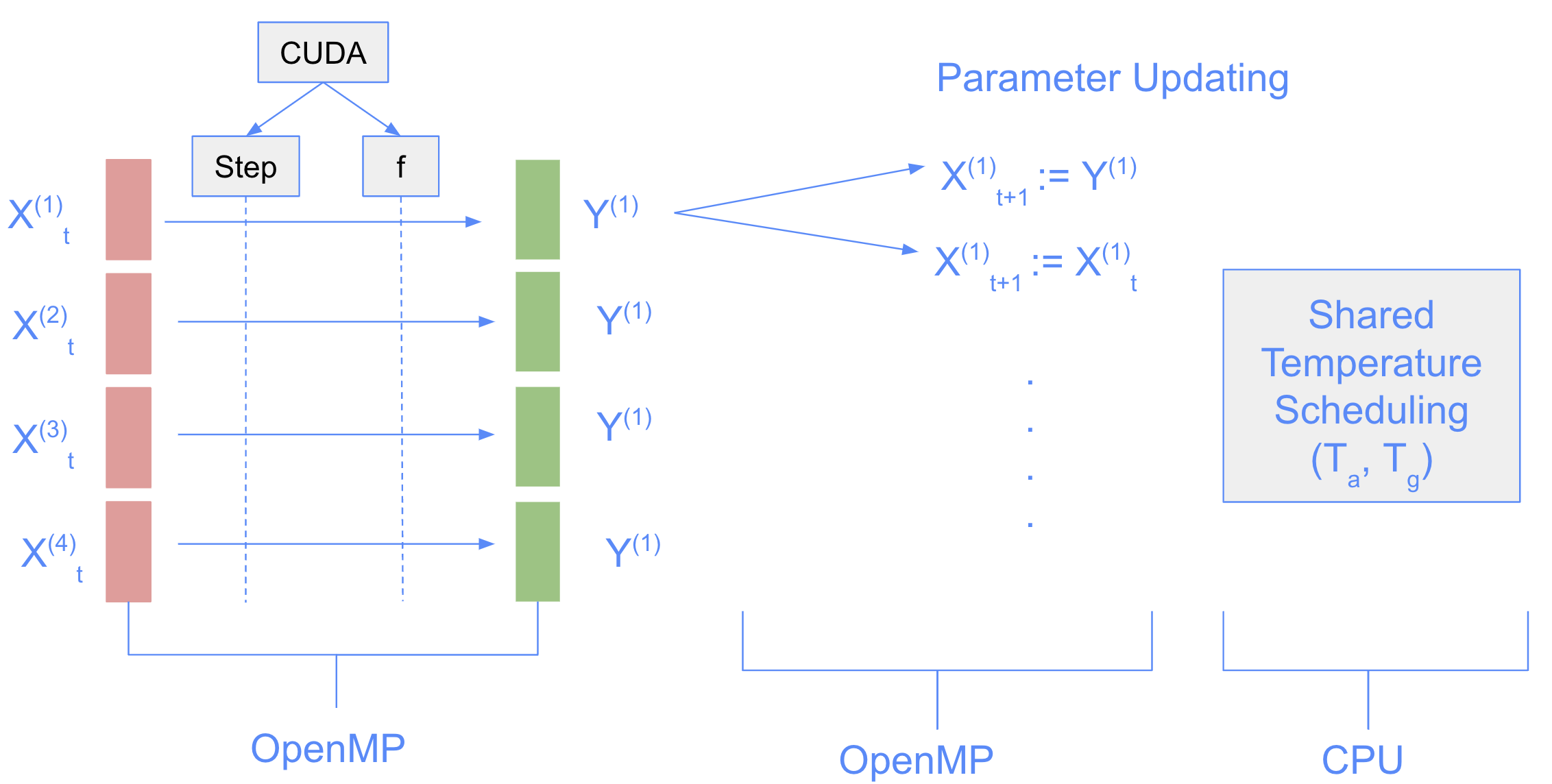
exploring parallelization models for simulated annealing
Parallelizing Simulated Annealing
How we accelerated global optimization by 11x using heterogeneous CPU+GPU computing and comparing cooperative vs. independent parallel algorithms
Global Optimization in Complex Landscapes
Traditional gradient-based optimization methods get trapped in local optima when dealing with complex, multi-modal landscapes. Simulated Annealing (SA) solves this by probabilistically accepting worse solutions, allowing escape from local traps to find global optima.
But how do we make SA faster using modern parallel computing? We compared two fundamentally different approaches:
Multi-Start Simulated Annealing (MSA)
- Multiple SA processes run completely independently
- No communication until final result selection
- Highly parallelizable with no synchronization overhead
Coupled Simulated Annealing (CSA)
- Multiple SA processes share information during optimization
- Periodic synchronization and parameter sharing
- Collective intelligence guides exploration
The Schwefel Function
We tested on the notoriously difficult Schwefel function:
\[f(x) = 418.9829d - \sum_{i=1}^{d} x_i \sin(\sqrt{|x_i|}), \quad x \in [-500, 500]^d\]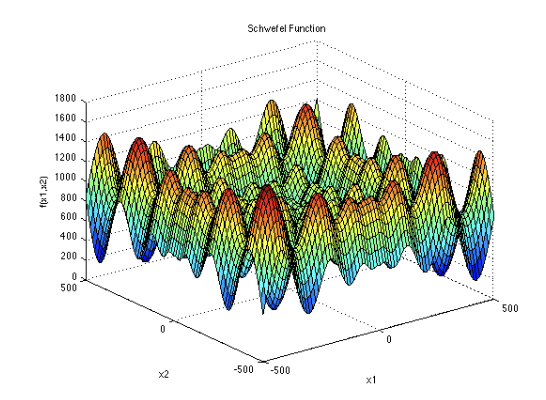
Why Schwefel: Large search space, many local minima, global minimum far from center, and crucially - linear separability allowing dimension-wise GPU parallelization.
Experimental Design
We systematically tested across four computational paradigms:
- Sequential: Single-threaded baseline
- OpenMP: Multi-threaded CPU parallelization
- CUDA: GPU acceleration for function evaluation
- Heterogeneous: OpenMP + CUDA combined
OpenMP Parallelization: Near-Linear Speedup
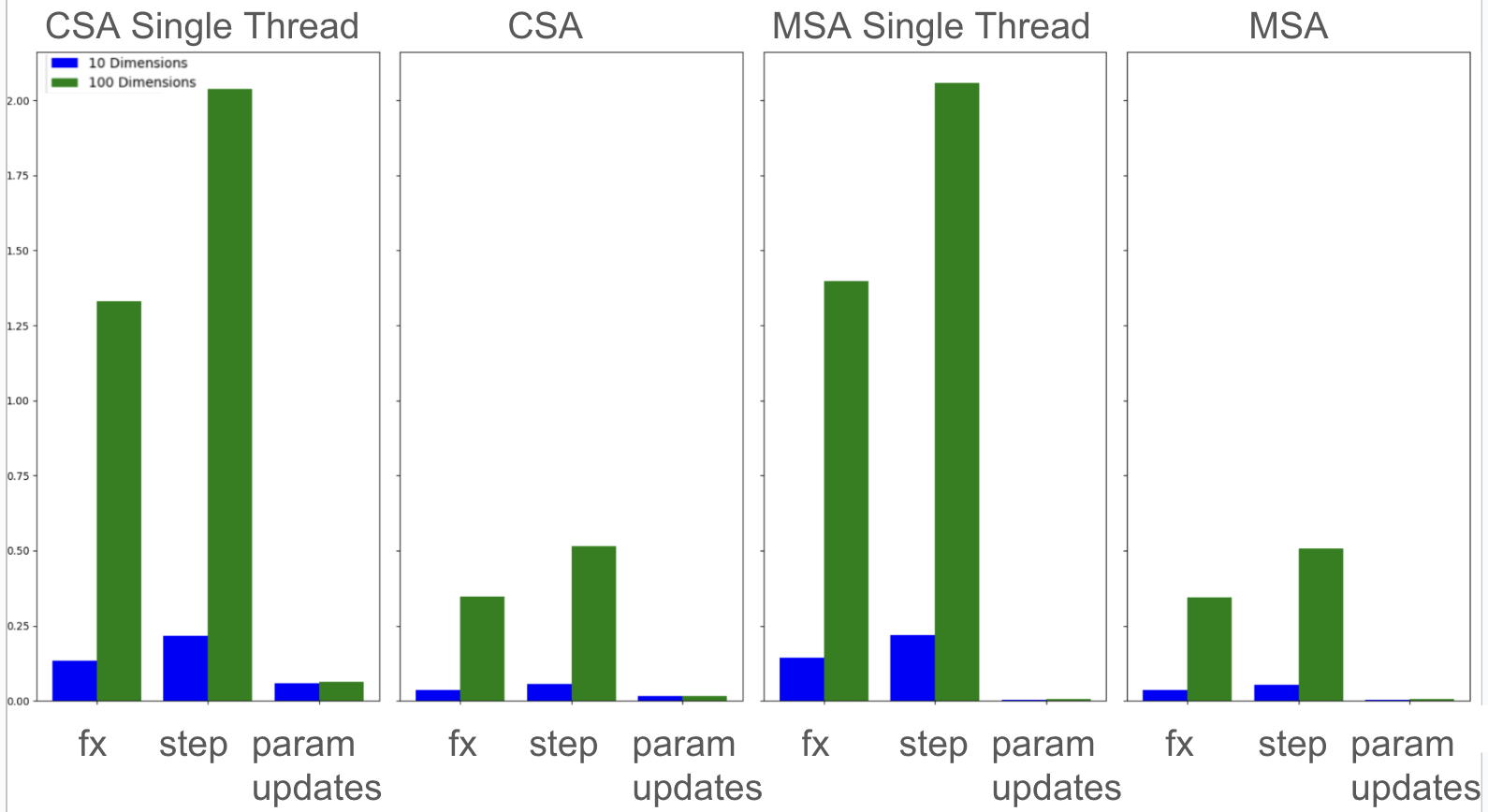
- 4x speedup with 4 threads (near-linear scaling)
- CSA overhead minimal: Parameter sharing costs negligible in parallel setting
- Surprising insight: Cooperation became essentially “free”
Heterogeneous Computing: Game-Changing Performance
| Configuration | MSA Single Thread | MSA Multi-Thread | CSA Single Thread | CSA Multi-Thread |
|---|---|---|---|---|
| CPU Only | 3,493,635 μs | 876,549 μs | 3,884,980 μs | 995,846 μs |
| GPU + CPU | 1,358,433 μs | 344,000 μs | 1,563,125 μs | 440,082 μs |
| GPU (Warped) + CPU | 1,208,433 μs | 321,389 μs | 1,413,214 μs | 400,981 μs |
Key Results:
- 3x improvement from heterogeneous computing alone
- Additional 20% boost from warp-level optimizations
- Total speedup: Up to 11x faster than baseline (3.49s → 0.32s for MSA)
Memory Bottleneck Discovery
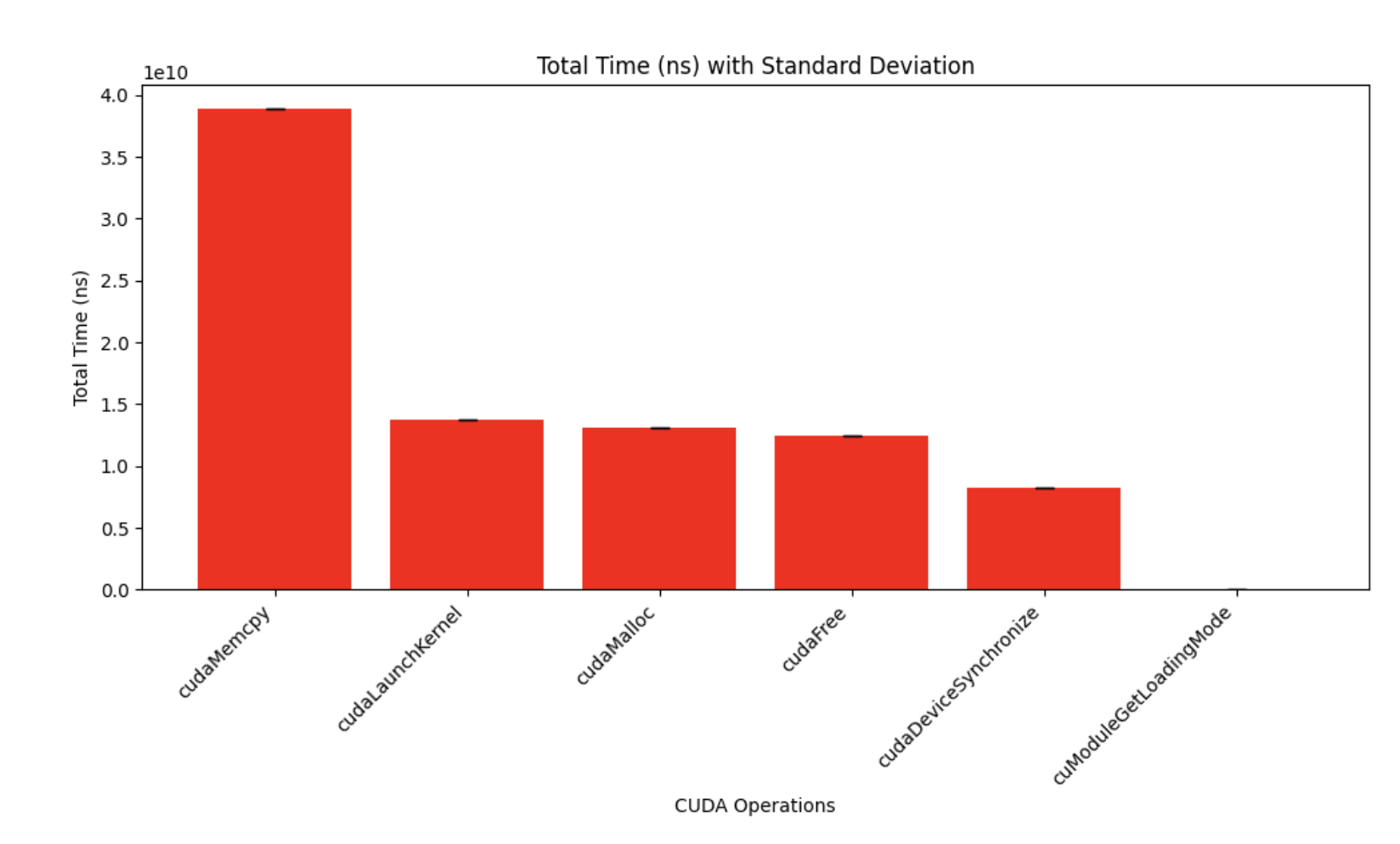
CUDA Profiling Revealed:
- 73% of GPU time spent on memory operations (copying, allocation, deallocation)
- Only 27% on actual computation
- Key insight: Memory management, not computation, determines performance
If we remember the roofline model, it is obvious here that we are in the nonoptimal part of the roofline model (i.e. not utilizing hardware effectively)
Implementation Highlights
Below are a couple of design details to show how we thought of this problem.
CUDA Kernel Design
// Exploit linear separability - one thread per dimension
__global__ void evaluate_schwefel_kernel(double* x, double* results, int d) {
int tid = blockIdx.x * blockDim.x + threadIdx.x;
if (tid < d) {
results[tid] = x[tid] * sin(sqrt(fabs(x[tid])));
}
}
// Warp-level reduction for efficient summation
__global__ void warped_reduction_kernel(double* partial, double* result, int d) {
// Use shuffle operations to avoid global memory synchronization
for (int offset = 16; offset > 0; offset /= 2) {
partial[tid] += __shfl_down_sync(0xffffffff, partial[tid], offset);
}
}
OpenMP Coordination
// CSA: Cooperative with careful synchronization
#pragma omp parallel for
for (int i = 0; i < num_processes; i++) {
while (!convergence) {
cuda_sa_step(process[i]); // GPU accelerated
#pragma omp barrier
#pragma omp critical
{ update_shared_parameters(process[i]); }
}
}
Conclusion
Our study demonstrates that heterogeneous computing can achieve dramatic speedups (11x) for global optimization, but success requires:
- Algorithm-hardware co-design: Matching computational patterns to architecture strengths
- Memory-first optimization: Focusing on data movement over raw computation
- Cooperative algorithms: Information sharing provides benefits when overhead is controlled
- Problem structure awareness: Mathematical properties (like linear separability) determine parallelization strategies
Key Finding: The combination of algorithmic cooperation (CSA) and heterogeneous computing (CPU+GPU) provides the best performance, achieving near-optimal solutions 11x faster than sequential approaches.
References
[1] Ge-Fei Hao, Wei-Fang Xu, Sheng-Gang Yang, et al. “Multiple Simulated Annealing-Molecular Dynamics (MSA-MD) for Conformational Space Search of Peptide and Miniprotein”. In: Scientific Reports 5 (2015), p. 15568. DOI: 10.1038/srep15568. URL: https://doi.org/10.1038/srep15568.
[2] S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi. “Optimization by Simulated Annealing”. In: Science 220.4598 (1983), pp. 671–680. DOI: 10.1126/science.220.4598.671. eprint: https://www.science.org/doi/pdf/10.1126/science.220.4598.671. URL: https://www.science.org/doi/abs/10.1126/science.220.4598.671.
[3] Latkin. A Simple Benchmark of Various Math Operations. Accessed: [2023]. Nov. 2014. URL: https://latkin.org/blog/2014/11/09/a-simple-benchmark-of-various-math-operations/.
[4] Simon Fraser University. Schwefel’s Function - Optimization Test Problems. https://www.sfu.ca/~ssurjano/schwef.html.
[5] Emrullah Sonuc, Baha Sen, and Safak Bayir. “A cooperative GPU-based Parallel Multistart Simulated Annealing algorithm for Quadratic Assignment Problem”. In: Engineering Science and Technology, an International Journal 21.5 (2018), pp. 843–849. ISSN: 2215-0986. DOI: https://doi.org/10.1016/j.jestch.2018.08.002. URL: https://www.sciencedirect.com/science/article/pii/S2215098618308103.
[6] Samuel Xavier-de-Souza et al. “Coupled Simulated Annealing”. In: IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 40.2 (2010), pp. 320–335. DOI: 10.1109/TSMCB.2009.2020435.
This research was conducted at Brown University in collaboration with Mason Lee, exploring high-performance global optimization. Complete implementation details and experimental data demonstrate the effectiveness of cooperative parallel algorithms in heterogeneous computing environments.